Introduction to Discrete Probability

So up till now we saw about how Cryptography was used in the past and how all the techniques were so poorly designed that some of them were weak enough to be cracked up by a smartwatch. But as time progressed, there developed a systematic way of designing ciphers and theories to support their securites were developed as well. Now all these theories and all "Modern Cipher Techniques" rely heavily on a mathematical concept "Discrete Probability" . So the topic for today's post will be a brief introduction to Discrete Probabilty.

Discrete Probability

Discrete probability is always defined over a universe U and in our case this universe is always going to be a finite set. IN our case this universe is going to be the set of all the n bits of strings which is here denoted by the

U : finite set = {0,1}ⁿ

Hence if the universal set is squared then  we will get the set of all the two bits of number which is 2 to the power 2. And more importantly there are basically two elements in the set U so the total number of elements in the U to the power N will be equal to the 2 to the power N. Hence if the value of n is 5 then the number of elements in the resultant set will be 32.

U² : {0,1}² = {00,01,10,11}

Now  a probability distribution is simply a function which is defined over the set of universe and is denoted by P and what it does is that it will assign a number between 0 to 1 to every element in the set of universe and that value which is between 0 to 1 is what we call the weight of that element and the necessary condition for the function is that every defined weight must sum up to be 1. That is if  I  sum up all the probabilities of every element in a universe X, its sum should be equal to 1.

So now getting back to our 2 bit universe, where we have taken all the possible outcomes for U² and now that we have all the elements of it that is {00,01,10,11} we can assign some probability to every element. SO lets say that the probability of the 00 outcome is ½ and for 01 is ¼ for 10 is 1/8 and similarly for 11 is 1/8. We can see that the sum of all the probabilities of the outcomes is equal to one. Hence we can say that this probability distribution is actually a probability distribution over N and is perfectly valid. Hence to formulate that we can say that:

So now we know what a probability distribution is and now lets have two classic examples of it. The first one is called the Uniform Probability distribution. As the name suggests that in uniform probability distribution will assign the same weights to every element in the universe. Hence the equation for the same will be :

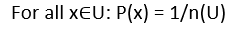
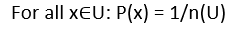
Here the n(U) denotes the number of elements in universe and as we want the same weights over all the elements we will divide 1 by the total number of elements. So of we look again at our previous example, we can see that the weights over all the two bits elements will be equal to ¼.

Another Probability Distribution which is quite famous is the point distribution at X₀.

So what the concept of the point distribution at X₀ does that it will assign all weights to any one element and all the other elements will have absolutely no weight over them. So the definition of the function is as follows:

So again seeing our example, we can set the weights of all the other elements as zero and for one element in the set, we can set it to 1. This way can safely assume that probability of the element that we assumed in our case will only be the possible outcome and no other outcome are favourable.

Now let me introduce the concept of Events.

Events:

So for a set A, which is subset of our universal set U, lets say that sum of probability of all the elements in set A lies between 0 to 1 where the sum of probability all the elements in the universal set is 1. For this instance the set A is called an Event.

Now, Here we have Uniform Distribution and we know that total number of elements in the universal set of 8 bits string is 2⁸ that is 256. Now we can calculate the total number of elements that has 11 as their  LSB (least significant bits). So we know that there would be 64 elements in that universal set which has 11 as their LSB. Now we can find the probability of the event A which is 64/256 which is 0.25. So we can say that the probability of event A is 0.25.

The Union Bound:

                The most common bound in the field of Discrete Probability is The Union Bound. So lets assume that there are two events, namely Event A₁  and A₂ , defined over the same Universal set U, the probability of the Union Bound of set A₁  and A₂ is always either less than or equal to the sum of individual probabilities of each event. That is if we revisit our previous example, We have a set of all the elements over a 8 bits universal set with 11 as their LSB₂, we can have another set in the same universal set with 11 as MSB₂. So we know that probability of each of the events is 0.25, and if we sum the probability of each event, we get 0.5. well in this case we had events were not disjoint event. i.e. they had some elements which occurred in both of the events. In such cases, we have the probability of the union of both events less than the sum of probabilities of individual events. While having disjoint set, it is equal.

Random Variables:

                Random Variable is basically a function defined over a Universal Set U and is mapped on another set V. So it basically takes value from the set U and gives the output to another set V induces the probability distribution on that set.

For example,

              

So lets say that there is a Random Variable X which takes an input of a n bit string and returns the LSB of that string. So we know that LSB will either be a 0 or a 1. So the probability of that Random Variable is 0.5.

More Generally,

Random Variable X induces the probability distribution of set V:  P[X = y] :=P[x^-1 (y)].

The Uniform Random Variable:

                The Uniform Random Variable X is just an identity function which returns the same value as the value which is given as an input. So basically the probability of all the Uniform Random Variables is just same as the Probability of all the elements in a Universal set U with a Uniform Distribution of the probability. So for e.g. lets say that r is a uniform random variable on {0,1}², and X = r₁ + r₂ ,

What is the probability of X = 2.

The answer to this is quite simple, X will be 2 only when both of the random variables will be equal to 1 and in this case it would be 0.25.

Randomized Algorithms:

We are all familiar with the Deterministic Algorithms where in a function, we get the same output every time for the same input that we provide. While in the case of Randomized Variables, we define a  function such that it will take input and along with that it will take an implicit argument of the random variable and then map the output according the that implicit argument that we provide. Also every time we run that algorithm, the other argument will be different. Hence for this case when we give the same input to function, we will not get the same output, rather we will get different outputs even for the same input we provide.

So to look at more broad way, we can say that there is an algorithm that takes some message m along with a random variable k as key, it will return the output from all the possible outputs for that message. For next time, the random variable will not be the same as the previous one, so even though we provided the same input, we will get different output which will be the encrypted form of that message.

Independence:

          The concept of independence says that when two events occurs, the occurrence of any one event should not reveal anything about the occurrence of the other event. So this means that when two events A and B occurs, the Probability of A and B is just the product of the probability of event A and the probability of the event B. That way we have no way to find out about the occurrence of the event by having the knowledge of only other event.

Concept of XOR:

XOR operation is one of the most common operation in the cryptography. XOR is basically the addition of two bits modulo 2. That means when while adding two bits, if both of the bits are same, it will return 0 and if both of the bits are dissimilar, it will return 1. For e.g. if A = 00111011 and B = 11010101, then A Ꚛ B (A XOR B) will be 11101110.

But why is XOR so common in cryptography? Well, the reason behind it is the very important property of XOR.

Theorem 1:  Let Y be a Random variable over U = {0,1}ⁿ , and X be a Uniform Random Variable over the same universal set. Then Z := Y Ꚛ X is a Uniform Variable over U.

Proof:

So for n = 1, we can say that y is a random variable on {0,1} and the probability of Y = 0 is lets say P₀  and Y = 1 is P₁. Similarly for X which is Uniform Random Variable, we know that probability of x = 0 is equal to probability of x = 1 which is 0.5. So now if we take the XOR of both of the distributions, i.e. Z = Y Ꚛ X, what we get is that the probability of Z = 0 is equal to Z =1 which is 0.5. Hence we can say that above theorem holds true for all such X,Y and Z.